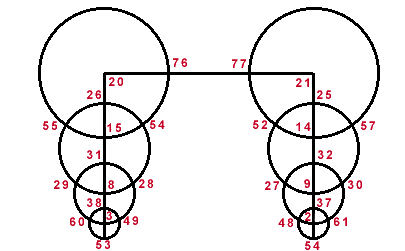
The straight lines sum to 78. The largest circles sum to 68. The second
largest circles sum to 85. The next largest circles sum to 105. The smallest
circles sum to 90. At the points where the circles intersect, the numbers
sum to an equal sum on the opposite side of the figure. (e.g. 18+15=16+17)

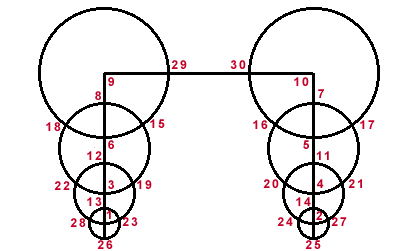
In the following solution, the straight lines sum to 68. The largest
circles sum to 95. The second largest circles sum to 109. The smallest
circles sum to 82. I like this solution better. It qualifies as more elegant
to me. If you add the vertical numbers in pairs together top to bottom,
each sum is 17. (e.g. 7+10, 6+11, 5+12, etc.) If you sum the vertical pairs
of numbers at the circles' intersections, you get a pattern. (16, 14, 16
on the left side and 14, 16, 14 on the right side.) The horizontal pairs
at the circle intersections sum to the same amount on the opposite side
as in the other solution.
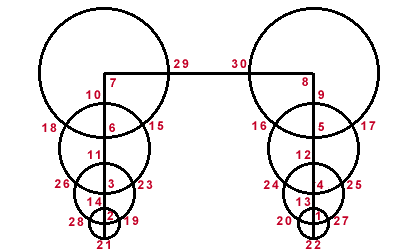
In the next arrangment, all the circles sum to 200. Can you create a
smaller magic sum? The lines have sum 194.