Chuck says: From where you start you have a 50% chance of losing immediately, a
25% chance of winning immediately, and a 25% chance of starting over.
We can ignore the case where you start over since it has no effect on
whether you eventually win or lose so I'd say you have a 1/3 chance of
winning and a 2/3 chance of losing.
say:
Cliff,
By a strict interpretation of the rules (no north and no
backtracking) there are 8 possible outcomes: 4 tunnel ends, and
4 dead ends (in the transverse sections.) If backtracking IS
allowed, the problem becomes more interesting and challenging.
Here is my solution. I express it in terms of the directions
taken by the marble. A choice is separated by a comma.
The 6 possible winning routes are:
E,E,ES,S,S
E,E,ES,WSES
E,E,S,S,SES
E,E,S,S,ES,S
E,S,E,ES,SES
E,S,E,ES,ES,S
Each choice has p=1/2, giving a sum of 3/16. Yet another
answer!
Actually, this is equivalent to Steve Brazzell's Analysis 3:
1/4 minus
the probability of getting stuck by going West just before
winning.
I've called this possibility deadend 4, below, and its
probability is 1/16.
Partly to satisfy myself that this logic is correct, and partly
out of curiosity, I calculated the probabilities of the other
possible outcomes. They sum to 1, which is encouraging!
Tunnel 1
========
W,WS,S
p=1/8
Tunnel 2
========
W,S,S,S
W,WS,ESES,S
E,S,S,WSWS
E,E,S,W,WS,WSWS
p=13/64
Tunnel 3
========
E,S,S,S,S
E,S,E,SWS
E,E,S,W,WS,S,S
E,E,S,W,WSW
p=17/128
Tunnel 4
========
p=3/16
Thus the probability of emerging from a tunnel is 83/128.
Deadend 1 (between tunnels 1 and 2)
=========
W,S,W
p=1/8
Deadend 2 (between tunnels 2 and 3)
=========
W,S,S,E
W,WS,ESES,E
p=1/8
Deadend 3 (between tunnels 3 and 4, left)
=========
E,S,S,S,E
E,E,S,W,WS,S,E
p=5/128
Deadend 4 (between tunnels 3 and 4, right)
=========
E,E,ES,S,W
E,E,S,S,ES,W
E,S,E,ES,ES,W
p=1/16
The probability of getting stuck in a deadend is 45/128.
So the possible outcomes, in descending order of probability,
are:
T2: 26/128
T4 (win): 24/128
T3: 17/128
T1,D1,D2: 16/128
D4: 8/128
D3: 5/128
Nick Hobson
Todd Redden says:
This solution involves plotting positions in the path beyond which the end
result is predetermined. If you get to any of these colored squares, the
end result is known, and no further inspection is necessary. All you
have to do is look at the percentage of remaining chances which can lead to
a given result at each turn.
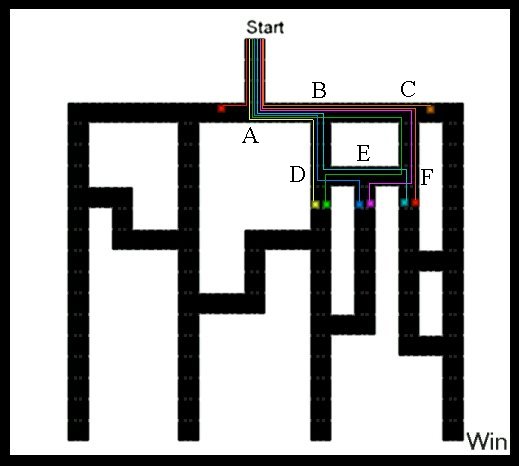
You lose 50% of the time at A by turning right.
Of the 25% that you go straight at B, you win 12.5% by going straight at C.
Of the 25% that you turn right at B, you lose 12.5% by going straight at D.
Of the 12.5% that you turn right at C, you win 6.25% by going straight at F,
and lose 6.25% if you turn right at F.
Of the 12.5% that you turn left at D, you lose 6.25% by turning right at E,
and you win 6.25% by turning right at F.
Adding things up, you win 25% of the time.
- Todd Redden
tmredden@snet.net
From Dominic :
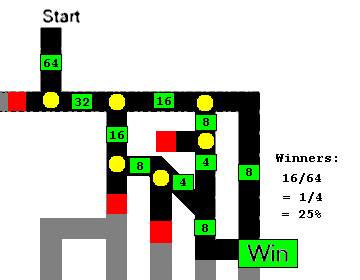It's much easier to understand if you simplify the maze. On this
modified map, I've marked places where a choice must be made with a
yellow circle, grayed out areas that have no effect on the solution, and
marked routes that guarantee failure in red. Looking at this map, there
are 6 places where a choice must be made. 2^6 = 64, so let's start by
dropping 64 marbles down the "tube" and assume that half will go down
each path at an intersection. We'll count how many make it to the end.
The green squares mark the number of marbles that have made it to that
point in the tube. Only 16 of the 64 will reach the finish line,
therefore the answer is 25%.
Similar to Todd's answer, but easier to follow.
-- Dominic Eldridge
From
"David" :
Hi Cliff.
Enjoyed the website, nice and challenging. The Tunnel, hmmm, seems everyone who has posted comments have analysed the heck out of it. Me, well by using a pencil to point to the tunnels on my screen and following the rules which says choices are move left, right or down and only these variants are allowed to either leave at the Win exit (or if you leave at the other exits and no neural stimulus - damn), the answer seems to be 5 routes will produce a win, and 4 will not - ergo 55.55% chance of winning.
kind regards,
David
From James Reimer :
I get a probaility of a win at 25% based on the
assumption that at each intersection there are only
two possibilities. Any time all the possibilities
along a branch result in failure, that branch is
eliminated. We are left with the sum of the
probabilities of all the winning branches. See the
analysis below. At each intersection, choices are
designated by a direction (Left, Right or Down) and a
probability, each time half of the previous
probability.
L-50% > > > > Failure
R-50% > D-25% > R-12.5% > D-6.25% > Failure
> R-6.25% > Win
> D-12.5% > > Failure
> R-25% > D-12.5% > L-6.25% > Failure
> D-6.25% > Win
> R-12.5% > > Win
The probabilities are added in the three winning
branches which amount to .0625 + .0625 +.125 = .25 or
25%
From Hans Mikelson:
Hi Clifford,
I get the same answer as those who are getting 25% chance of winning.
Attached is a diagram which hopefully explains my solution.
Bye,
Hans Mikelson
P.S. I've been a big fan of your books for many years!
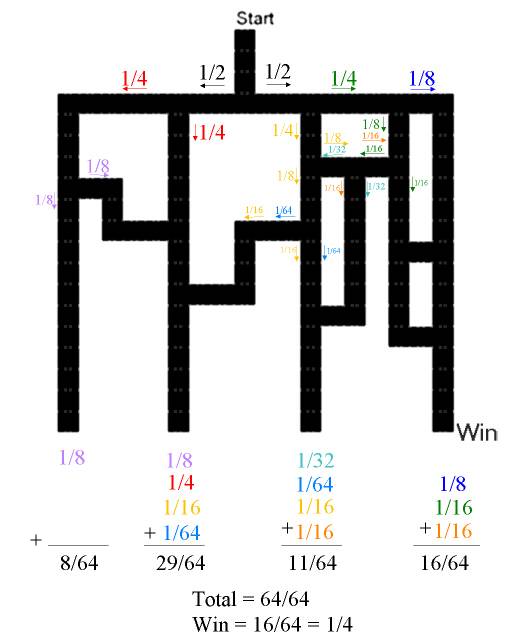
From Larry Kubicz:
Cliff,
Here's my analysis of the tunnel puzzle. I took a hands-on approach, which I figured would get to the heart of the matter. I went under the assumption that backtracking wasn't allowed.
For this, I borrowed the diagram supplied and labeled by David Jones. I just added another label, Z, at the intersection just north of Win. If you draw this out, it helps to draw little arrows to track the numbers going hither and yon through the tunnels.
I assembled 64 of my closest imaginary friends at the Start point. At each branch, half of those entering will take one fork, and half the other, which is why I chose a power of 2.
At A, 32 of our brethren will head west, never to be seen again. The rest head east.
At B, the remaining 32 will split: 16 heading east for C, and 16 heading south for D.
At C, the 16 will split: 8 heading east for Y, and 8 heading south for F.
At D, the 16 will split: 8 heading east for E, and 8 heading south for oblivion.
At E, the 8 from D will split: 4 continuing east for F, and 4 heading south for oblivion.
At F, th 8 from C will split: 4 continuing south for X, and 4 heading west for oblivion. The 4 from E will join up with the 4 from C, making a total of 8 heading south for X.
At X, the 8 from F will split: 4 continuing south to Z, and 4 heading west for Y.
At Y, the 8 from C will split: 4 continuing south to Z, and 4 heading west for X. This latter 4 will join up with the 4 from F, making a total of 8 proceeding south to Z.
At Z, we'll have 8 from Y joining 8 from X, for a total of 16, which yields the usual 16/64=25%.
BUT, perversely, half of those from Y will decide to turn west into a dead end. This leaves 12 to head south to Win, where they can mourn their lost brethren. 12/64=18.75%.
Larry Kubicz
From "George Greenwade":
I agree with the answers of .25 for a probability of winning and offer a textual presentation of the logic, based on the figure provided by David Jones at the start of the solutions.
This is a probability question that begs the question of is it better to look at the probability of an event happening (p) or the probability of an event not happening (1-p), but the bottom line is that the sum of two exclusive events (win/lose) must equal 1.
At point A, each path (east or west) occurs with equal probability of .5. If the westward path is chosen, it is impossible to get to WIN as neither tunnel P nor Q connect to WIN in a fashion consistent with the constraints of no northward movement.
Therefore P(win EAST) = 0 and the total cumulative probability (cumP) of winning (cumP(win)) is reduced to 0.50 at best and cumulative probability of losing (cumP(lose)) is at least 0.50.
If the eastward path is chosen, tunnels B, C, and R are possible, but not equiprobable.
Given three southbound tunnels for the eastbound traveler, the probability of being included in tunnel B is .25, tunnel C decays to .125, and tunnel R accepts all remaining travelers and is .125.
The critical point on tunnel B is D, the only possible way to achieve WIN. With equiprobable changes in direction at D, .5 of the .25 (.125) will continue southward to not satisfy the WIN criteria. Therefore, .25 of the total originally eastbound travelers will fail to WIN (.25*.5) =.125 will exit due south of B and may be added to the westbound failures, providing cumP(loss)=.625
For the .125 who travel east at point D, one half (.0625) will go south at point E, return to tunnel B and fail to win, providing cumP(loss)=.6875. The remaining eastbound travelers will get to point F and must eventually get to WIN, providing cumP(win)=.0625
Those travelers who go southbound at point C (.125) face one critical point, F. Again, given an equiprobable movement at this point, half (.0625) will go west, ending their trip at the foot of tunnel Q or tunnel B, providing cumP(loss)=0.75 and cumP(win)=.125
For the .125 who travel east and end at point R, the probability of winning is 1 as there is a turn point at Y, although it is not a critical point as northbound travel is disallowed at the terminal X (they behave as if they were simply dropped straight down tunnel C, which ultimately returns to tunnel R.
Net result cumP(loss)=.75 and cumP(win)=.25
---------------------------------------------------------
An aside which I will explore more as time allows:
Provided that A is a one way door (travelers may not exit the system via the entrance), backtracking is allowed (i.e., at a point such as P, eastbound travelers may simply take a 180 degree turn and travel west) and full movement is allowed (i.e., northward is permissible within the system), I hypothesize that this problem reduces to a decay formula which, at the limit, becomes a half-life formula based on the outcomes (the exits). Note that this does not alter the simple solution above as the movement becomes equiprobable at each stage with only one possible winner (1 winner out of 4 possibilities or 1/4 or 0.25).
George
From Robert G. Brown:
The choice is: work on your puzzles or grade finals. Hmmmm.
So, in Tunnels of Callicrates, there appear to be two distinct families
of solutions. In one, the trajectories are self avoiding (that is, when
one hits a junction, one is not allowed to retrace one's steps back up
the tunnel from which one came). In that case the solution is fairly
pedestrian, I think -- just counting the fraction that lose at each
signficant junction (one where one branch definitely loses or definitely
wins) and tracking marble or alien flux leads to 25% who reach win,
unless I miscounted (which is always a possibility:-).
However, the fiendish problem arises if one imagines that the alien
enters a spinning wheel at each junction what whirls, opening on any of
the TWO OR THREE possible pathways that lead away from each junction.
That is, if at each junction the alien has an equal probability of
retracing their steps back the way they came (provided the route back is
permitted), one starts getting truly horrible series expansions for the
probability flux that wins or loses summing over significant junctions,
stuff like 1/2\sum_{n=1}^\infty (1/6)^n ultimately added to the 1/2 flux
to the right at the very first junction from the series of successive
reflections between that first junction and the first junction on the
left, which is ITSELF further modified by higher order "multiple
scattering" contributions from reflections from the first junction on
the RHS and so forth. Yuk.
I actually am a statistical mechanic and do Monte Carlo, and it seems
like the best way to find a very good approximation to the solution in
this case (if one isn't attached to doing immense amounts of mindless
algebra, which I actually am but can't take THAT much time away from
grading finals:-) is to create a simple hash of significant junctions in
e.g. perl, populate the toplevel junction and create stochastic
trajectories through to eventual certain win or loss (e.g. 100% of the
traffic to the left at the first junction on the left can never win),
and just plain count the number that make it to "win". At the moment
I'm having a hard time finding an intuitive hat, but given the symmetry
of the of the first two junctions two the right and left of the primary
one and the EXTRA junction on the right, I would expect a small
additional probability flux to the lossy side from the SECOND junction
on the right hand set of pathways and so an ultimate probability of
winning somewhat less than 1/4. Can't quite make up my mind about flux
conservation at e.g. the central link along the box between the first
two right hand downward pathways -- clearly reflections from flux down
the first RH pathway will increase the net loss along this pathway (I
think) but the loss will be ameleorated somewhat symmetrically by
reflections from the flux down the second path at the first junction.
I assume that you probably know the algebraic answer to this one. If
you care I'd be glad to share the results of my simulation, if I end up
writing one.
BTW, you might edit the problem to make it clear whether your use of the
word "either" in "equally likely to choose either route" is binary (self
avoiding) or not (the more interesting problem above). The common usage
is binary (either A or B, but not EITHER A or B or C) and English
shouldn't be an obstacle to a nice little mathematical problem.
rgb
--
Robert G. Brown http://www.phy.duke.edu/~rgb/
Duke University Dept. of Physics, Box 90305
Durham, N.C. 27708-0305
From Ben Daglish:
Has anyone done this? - I couldn't see it on the page....
Seems the obvious thing to do. (Use a fixed font :) )
*
*
100%
*
*************************************
* * * * *
20% 20% 20% 20% 20%
* * * * *
* * * * *
* * ***10%**** *
* * * * * *
*10%* * 15% 10% 15% *
* * * * * * *
* * * * * **********
* ****** *7.5%* * * * * * * * * 17.5% 17.5%
10% 30% * 7.5% * * *
* * * * * * *
* ***** ***** **********
* * * * *
* * * * *
* * * * *
10% 37.5% 17.5% 17.5% 17.5%
Therefore it's a 17.5% probability, assuming backtracking / never taking possible North tracks.
Cheers,
Ben Daglish
Graham says:
In all your tunnel problems, your solvers would find life much simpler is they started out with 2^n (assuming binary gates and n big enough - usually n=5 is enough) marbles, and then counted how many go in which direction at each gate.
I'm also interested in the faith placed in simulations - if you base the simulations on the assumptions you originally used then the simulation is always going to prove you were right. Logic always does that.
Interesting page, though.
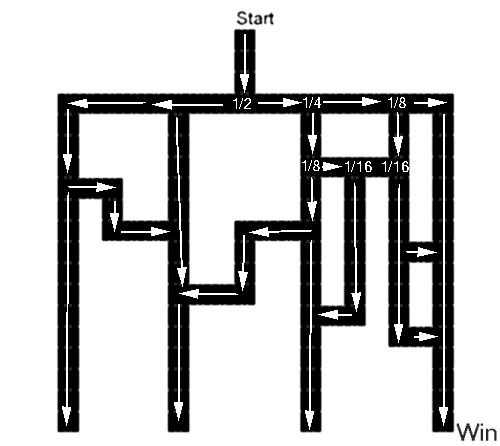Gordon says:
The marble drops, first choice, east or west. Each has 1\2 chance. West 1\2 is sure failure. Lets asume the east 1\2 is taken. Second choice south or continue east. Each has 1\2 of the remaining half or 1\2 chance. Lest expand on the south 1\4 first. Third choice south or east. Each has 1\2 of the remaining 1\4 chance. The south 1\8 is sure failure. Lets asume east is chosen. The fourth choice is to continue east or to turn south. Each has 1\2 chance of the remaining 1\8. The south choice is sure failure. The east choice is sure success. This gives 1\16 chance of winning if the second choice is south. Now if the second choice is east the third choice is to continue east or south. Each has 1\2 of the remaining 1\4 chance. If the south 1\8 is chosen the fourth choice is to continure south or to turn west. Each has 1\2 of the remaining 1\8 chance. The west 1\16 is sure failure where the south 1\16 is sure success. That being said there are two seperate ocassions where there is a 1\16 chance of success and one where there is a 1\8 chance. Therefore there is a 1\4 chance of success. Alternately 1\2 have no chance. Choice two 1\16 of that 1\4 that drops south win that leaves 3\16 that loose. Choice three 1\16 of the 1\8 that drop south win that leaves 1\16 losing. Do some addition of the losers 1\2 + 3\16 + 1\16 = 3\4. The only thing that could complicate things more is if you added in the possibility of reversing direction. If you want to see try that one e-mail me back. Not clear enough?
Bob Ewell says:
This analysis uses the diagram from the very first, which, except for a minor error that the author made, is the correct approach. Moreover, I have completely analyzed the paths through the tunnels (with no backtracking) to ensure that the sum of all paths’ probabilities is 1.0. We don’t need to consider all possible paths--we need only trace a path until its outcome is certain.
First path: go west at A, and you lose. You have a 1/2 probability of doing that. Nothing else on the west side of the start is material since there is no way to get back to the win tunnel from there.
Second path: ABD, going south at D. You lose. Probability is 1/8
Third path: ABDE, going south at E. You lose. Probability is 1/16
Fourth path: ABDE, going east at E. You win. Probability is 1/16
Fifth path: ABCF, going west at F. You lose. Probability is 1/16
Sixth path: ABCF, going south at F. You win. Probability is 1/16
Seventh path: ABCR: You win. Probability is 1/8
The sum of all probabilities = 1/2 + 2 x 1/8 + 4 x 1/16 = 1.0
Of those, the ones corresponding to a win are one at 1/8 and two at 1/16 = 1/4.
This solution is complete and correct. If there is no backtracking, there is no room for doubt or discussion. We have a complete sample space with the probabilities adding to 1.0.
Tunnels of Callicrates, the solution of
---------------------------------------
Written 2008-03-08 by Anders Hallström
Dear Cliff,
I find the Tunnels of Callicrates an interesting problem
and I have prepared a solution for it.
We have seen that the solution depends heavily on how
different people interpret the given conditions.
Reading your description and not peeking at other peoples's work,
I naturally, without thinking much about it, made the most liberal
interpretation of when there is a "choice".
I assumed a corner is to be seen as a junction where the marble can bounce.
I also assumed that the initial junction (node A below)
continues to be seen as a junction although we can never go up again.
This, I believe, gives the hardest and most challenging problem.
Although I prepared this solution independently
before looking at other people's work,
I will now, for everybody's convenience,
reuse the labelings that David Jones used in his analysis.
(Adding G,H,I,J)
(Note that the uninteresting parts of the maze have been pruned off!)
|
|
P --- Q --- A --- B ------- C --- R
| | | | |
| | | | |
| | D -- E -- F |
| | | | | |
| | | | | |
I J G H X Y
(LOSE) (LOSE) (LOSE)(LOSE) (WIN) (WIN)
Solution to worst-case interpretation (I1):
------------------------------------------
Note that we now have a game that involves potentially infinite bouncing.
However, the probability of getting stuck on a level for a long time
is very low. The probability of never falling down is zero.
The ride could however go on for an unlimited (but finite) time.
Consider pA = a sort of generalised probability of reaching node A,
*including* all possible repetitions. Such a generalised probability
can be larger than 1. Indeed, we start at node A with probability 1
and we may revisit later, so pA > 1.
Instead of attempting to compute sums of infinite series,
we are going to solve for these node probabilities indirectly.
Transition probabilities:
pAQ = 1/2 = pAB, pQA = 1/3 = pQJ = pQP, pPQ = 1/2 = pPI, etc.
pIP = pJQ = pGD = pHE = pXF = pYR = pDB = pFC = 0
Net probability flow from A to Q:
pAQtot = pA*pAQ - pQ*pQA = pA/2 - pQ/3
This represents the probability of ever leaving node A
towards node Q and not returning.
From Q to P:
pQPtot = pQ*pQP - pP*pPQ = pQ/3 - pP/2
From P to I:
pPItot = pP*pPI - pI*pIP = pP/2 - 0
By flow conservation, net flow from Q to P must equal flow from P to I.
Also, since this is the only way to reach node I, pI = pPItot.
pI is the true probability of reaching node I since
node I is terminal, no bouncing, no repetitions possible.
This is true of all terminal nodes I,J,G,H,X,Y.
pQPtot = pPItot = pI
pQ/3 - pP/2 = pP/2
pQ/3 = pP
pI = pP/2 = pQ/6
pJ = pQJtot = pQ*pQJ - 0 = pQ/3
Another flow conservation equation:
(This is not entirely unlike Kirchhoff's current law for electrical circuits)
pAQtot = pI + pJ
pA/2 - pQ/3 = pQ/6 + pQ/3
3/6*pA = pQ(1/6 + 2/3) = 5/6*pQ <=> 3*pA = 5*pQ <=> pQ = 3/5*pA
pI = pA/10
pJ = pA/5
By symmetry, R and C behave as P and Q:
pC/3 = pR
pY = pRYtot = pR/2 = pC/6
pCFtot = pC*pCF - 0 = pC/3 { Note however that pF will be something else }
pBDtot = pB*pBD - 0 = pB/3 { Note however that pD will be something else }
pBCtot = pB*pBC - pC*pCB
pBCtot = pCFtot + pY
pB/3 - pC/3 = pC/3 + pC/6
2*pB = 2*pC + 2*pC + pC = 5*pC <=> pC = 2/5*pB
pABtot = pA*pAB - pB*pBA
pABtot = pBDtot + pCFtot + pY
pA/2 - pB/3 = pB/3 + pC/3 + pC/6
pA/2 = 2/3*pB + pC/2 = 2/3*pB + pB/5 = pB(10/15 + 3/15) = pB(13/15)
pB = 15/26*pA
pY = pC/6 = 2/30*pB = pB/15 = pA/26
pCFtot = pC/3 = 2*pY = 2/26*pA = pA/13
pBDtot = pB/3 = 5/26*pA
Eventually we have to go down one of the five pitfalls:
1 = pI + pJ + pBDtot + pCFtot + pY
1 = pA(1/10 + 1/5 + 5/26 + 1/13 + 1/26) = pA(3/10 + 8/26) = pA(3/10 + 4/13) =
= pA(3*13 + 4*10)/(10*13) = 79/130*pA
pA = 130/79 { > 1 as already established }
pI = pA/10 = 13/79
pJ = pA/5 = 26/79
pBDtot = 5/26*pA = (5*130)/(26*79) = 25/79
pCFtot = pA/13 = 10/79
pY = pA/26 = 5/79
Now we move to "stage 2" to find pG, pH, pX.
pG = pDGtot = pD*pDG = pD/2
pH = pEHtot = pE*pEH = pE/3
pX = pFXtot = pF*pFX = pF/2
pDEtot = pD*pDE - pE*pED = pD/2 - pE/3
pFEtot = pF*pFE - pE*pEF = pF/2 - pE/3
Flow equations:
pBDtot = pDGtot + pDEtot
25/79 = pD/2 + pD/2 - pE/3 = pD - pE/3
pCFtot = pFXtot + pFEtot
10/79 = pF/2 + pF/2 - pE/3 = pF - pE/3
pEHtot = pDEtot + pFEtot
pE/3 = pD/2 - pE/3 + pF/2 - pE/3 <=> 2*pE = pD + pF
2*pE = pD + pF = 35/79 + 2/3*pE
4/3*pE = 35/79
pE = (3*35)/(4*79) = 105/316
pD = 25/79 + pE/3 = 25/79 + 35/316 = 135/316
pF = 10/79 + pE/3 = 10/79 + 35/316 = 75/316
pG = pD/2 = 135/632
pH = pE/3 = 35/316
pX = pF/2 = 75/632
Finally:
p_WIN = pX + pY = 75/632 + 5/79 = (75 + 5*8)/632 = 115/632 { ~= 1/6 }
p_WIN ~= 0.18196
Solution to worst-case interpretation (I1) using David Jones' method:
--------------------------------------------------------------------
Letter Z denotes probability to win at node Z.
I = J = G = H = 0
X = Y = 1
R = 1/2*Y + 1/2*C = 1/2 + C/2 <=> 2R = 1 + C
C = 1/3*B + 1/3*F + 1/3*R
B = 1/3*A + 1/3*D + 1/3*C
F = 1/2*X + 1/2*E = 1/2 + E/2 <=> 2F = 1 + E
E = 1/3*D + 1/3*H + 1/3*F = D/3 + F/3 <=> 3E = D + F
D = 1/2*G + 1/2*E = E/2 <=> 2D = E
6E = 2D + 2F = E + 2F
5E = 2F = 1 + E
4E = 1 <=> E = 1/4
E = 1/4
D = E/2 = 1/8
F = 1/2 + E/2 = 1/2 + 1/8 = 5/8
C = B/3 + 5/24 + R/3
6C = 2B + 5/4 + 2R = 2B + 5/4 + 1 + C <=> 5C = 2B + 9/4
B = A/3 + 1/24 + C/3
5C - 9/4 = 2B = 2A/3 + 1/12 + 2C/3
15C - 27/4 = 2A + 1/4 + 2C
13C = 2A + 1/4 + 27/4 = 2A + 7
P = 1/2*I + 1/2*Q = Q/2 <=> 2P = Q
Q = 1/3*P + 1/3*J + 1/3*A = P/3 + A/3 <=> 3Q = P + A
6Q = 2P + 2A = Q + 2A
5Q = 2A
A = 1/2*Q + 1/2*B
10A = 5Q + 5B = 2A + 5B <=> 8A = 5B
3B = A + 1/8 + C
24A = 15B = 5A + 5/8 + 5C <=> 19A = 5C + 5/8
We now have the two-equation system
13C = 2A + 7 <=> 5*13C = 10A + 35
19A = 5C + 5/8 <=> 13*19A = 5*13C + 13*5/8
13*19A = 10A + 35 + 13*5/8
A(13*19 - 10) = 35 + 65/8 = 35 + (64 + 1)/8 = 43 + 1/8
13*19 = 13(20 - 1) = 260 - 13 = 247
237*A = 43 + 1/8 = (43*8 + 1)/8 = 345/8
A = 345/(8*237) = (115*3)/(8*79*3) = 115/(8*79) = 115/632
A ~= 0.18196
How nice, we have now reached the same result with two different approaches.
This suggests that both methods are valid.
Solution to next-worst-case interpretation (I2):
-----------------------------------------------
David Jones' submitted analysis differs from my interpretation I1
only in that node A is not regarded as a junction after the first fall.
See David Jones' analysis (although I have not double-checked it);
A = 161/880 ~= 0.183
If you would also consider corners as no choice, see next section.
Solution to limiting interpretation (I3):
----------------------------------------
Now let's also investigate a more strictly limiting
interpretation of when there is a "choice";
Backtracking allowed but only where there is an "effective" choice.
In this interpretation, corners represent no choice.
Corners are simply passed just as a straight corridor.
Also junctions where no forking is allowed represent no choice.
Thus nodes A, D and F are effective junctions only when falling down,
otherwise A is seen as a simple corridor and
D and F are seen as simple corners.
Nodes P and R disappear as junctions, and
nodes A, D and F disappear unless you fall from above.
I think Davy's method will be the most convenient now.
Letter Z denotes probability to win at node Z.
I = J = G = H = 0
X = Y = 1
C = 1/3*B + 1/3*F + 1/3*Y = B/3 + F/3 + 1/3
B = 1/3*Q + 1/3*D + 1/3*C
F = 1/2*X + 1/2*E = 1/2 + E/2
E = 1/3*G + 1/3*H + 1/3*X = 1/3
D = 1/2*G + 1/2*E = E/2 = 1/6
F = 1/2 + 1/6 = 4/6 = 2/3
C = B/3 + F/3 + 1/3 = B/3 + 2/9 + 1/3 = B/3 + 5/9
B = Q/3 + (1/3)*(1/6) + C/3 = Q/3 + C/3 + 1/18
3B = Q + 1/6 + C = Q + 1/6 + B/3 + 5/9
B(9 - 1)/3 = Q + (3 + 10)/18
8/3*B = Q + 13/18 <=> 6*8B = 18Q + 13
Q = 1/3*I + 1/3*J + 1/3*B = B/3 <=> 3Q = B
18Q = 6B
48B = 6B + 13 <=> 42B = 13 <=> B = 13/42
Q = B/3 = 13/126
A = 1/2*Q + 1/2*B = B/6 + B/2 = 2/3*B = (2*13)/(3*42) = 13/(3*21) =
= 13/63
A ~= 0.2063
Solution to trivial interpretation (I4):
---------------------------------------
With no backtracking allowed,
there are multiple ways to reach the simple solution
A = 1/4 = 0.25
as many have shown already.
This is the highest result you can get with any "reasonable"
interpretation of the problem.
Suggestions that A may be as large as 0.4 are not valid.
Return to
Cliff Pickover's home page which includes computer art, educational
puzzles, higher dimensions, fractals, virtual caverns, JAVA/VRML, alien
creatures, black hole artwork, and animations. Click here
for a complete list of over 20 Cliff Pickover books.
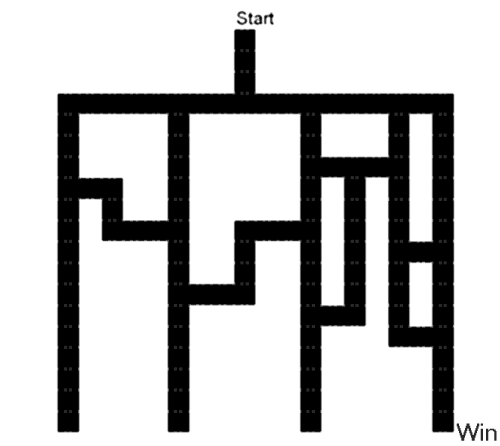
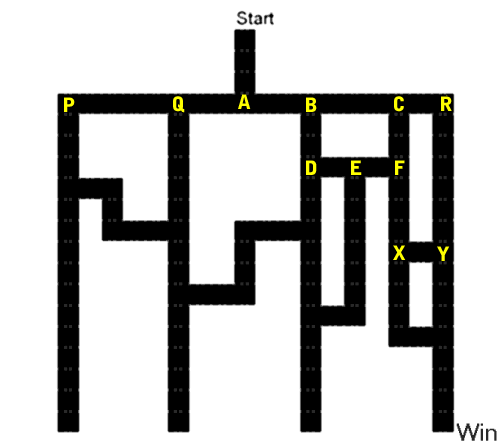To start the problem off, lets label each intersection
(or choice) with a letter. The diagram shows points
A-F, X, and Y. Second, to make things slightly
easier, notice that when you get to either X or Y that
you have won. You cannot lose from either of these
points regardless of how you got there. Since we will
be measuring probabilities, it is easier to measure
them going to points X and Y rather than to the final
destination. Points P, Q, and R are only used in the
second problem.
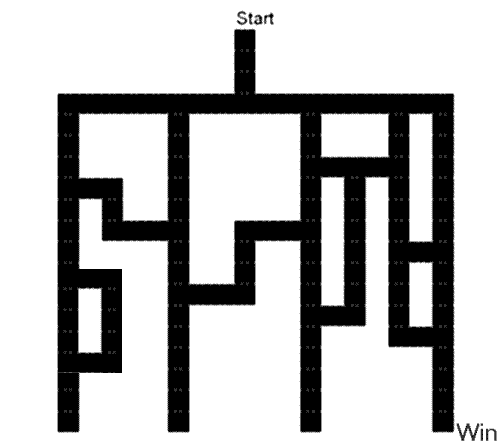
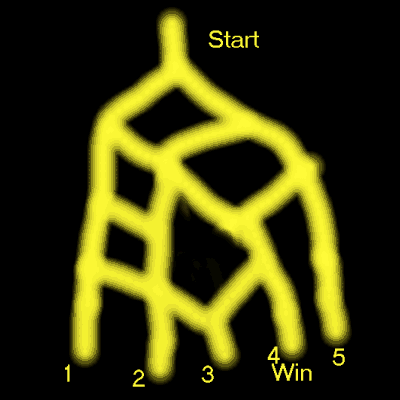
According to some people's false logic you, there is equal probability that
the marble will get to the rightmost or leftmost exits. Doesn't it look funy
to you? Yes, there are 6 different pasages, but don't forget that they don't
have the same probability of occuring.
The answer should be: on each junction the marble will go in the right
direction with 50% probability. So, if we have four junctions, the answer is
p=0.5*0.5*0.5*0.5=0.0625=6.25% and not 1/6 as you said.
Thanks for your enjoyable site. It's delitious for Math-lovers. Jack
Kuperman.
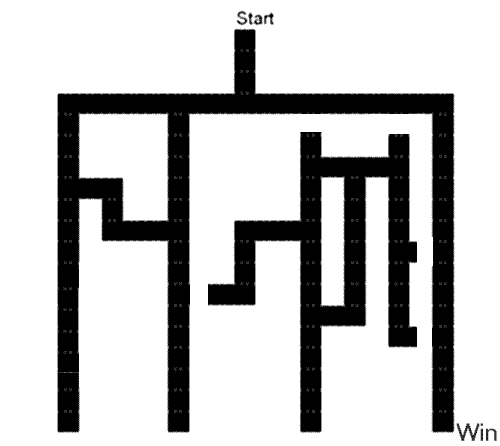
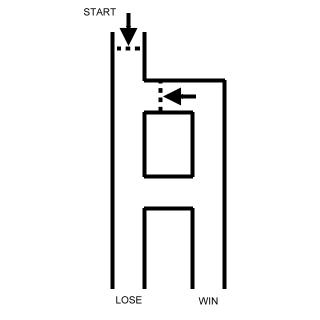The story is slightly different too. In this case, the
evil puzzlemeister, Clickover, has been feeding you tequila
shooters all evening. Then, he dropped you at the start
gate of the tunnel. Since it is completely dark, and you
are mentally obliterated by this point, you are only
capable of making random turns whenever you encounter
a fork in the tunnel.