Contact |
Books |
Home |
Contact |
Books |
Home |

|
The Mobius Strip
Dr. August Mobius's Marvelous Band in
Mathematics, Games, Literature, Art, Technology, and Cosmology
Thunder's Mouth Press, 2006 Acclaimed popular science writer Clifford Pickover explores the weird world of the shape made famous by M. C. Escher "Pickover inspires a new generation of da Vincis to build unknown flying machines and create new Mona Lisas." -- Christian Science Monitor "Bucky Fuller thought big, Arthur C. Clarke thinks big, but Cliff Pickover outdoes them both." -- WIRED "A perpetual idea machine, Clifford Pickover is one of the most creative, original thinkers in the world today." -- Journal of Recreational Mathematics
|
The Mobius Strip: |

|

Mobius Strip with Penrose Tiling Courtesy of Teja Krasek .
.
.
.
|
Table of ContentsIntroductionIn which we encounter a "hole through a hole in a hole," topology, Mobius strips, the desiccated skull of Mobius, Franz Gall, the recycling symbol, Mobius beer, the Mobius Flip, Max Bill's "Endless Ribbon," Gustavo Mosquera, Eternal Sunshine of a Spotless Mind, Mobius strip metaphors, Mobius strips in religion, Eugene Ionesco's play The Bald Soprano, the cerebral Mobius strip, and the Acme Klein Bottle. Chapter 1 Mobius MagiciansIn which we encounter Mobius illusions, gospel magic, the Mobius treadmill puzzle, Mobius's place in history, and my boyhood introduction to the marvelous band. Chapter 2 Knots, Civilization, Autism, and the Collapse of SidednessIn which we encounter ants inside spheres, Mobius dissections, sandwich Mobius strips, Ljubljana ribbons, Lord Kelvin's vortex knots, trefoil knots, New York lawyer and part-time topologist Kenneth Perko, the mystery unknot, Asperger's syndrome, Wolfgang Haken's unimplementable knot algorithm, the triquetra, the occult TV show "Charmed," Led Zeppelin, The Book of Kells, knots in proteins, Borromean rings, knots as catalysts of civilization, the alien knot puzzle, and Mobius aliens. Chapter 3 Mobius the ManIn which we encounter Mobius's family tree, simultaneity in science, Schulpforta, Paul Julius Mobius, Mobius syndrome, Johann Benedict Listing, the "king with five sons" problem, Mobius's mathematical output, Karl August Mobius, the false dawn animal, the Mobius maze puzzle, and Mobius licentiousness. Chapter 4 Technology, Toys, Molecules, and PatentsIn which we encounter the Rhennius machine, Roger Zelazny's Doorways in the Sand, Mobius patents and toys, Mobius molecules, mathematics patents, lemniscates, astroids, Reuleaux triangle drill bits, conveyor belts with twists, surgical retractors, Mobius electrical components and train tracks, knot patents, the metaphysics of shoelaces, chirality, Lipitor, Paxil, Zoloft, Nexium, Thalidomide, Advil, enantiomers, Methanobacterium thermoautotrophicum, Mobius plant proteins that induce labor in African women, Mobius crystals, the Noah's ark puzzle, and Mobius strips in fashion and hair style. Chapter 5 Strange Adventures in Topology and BeyondIn which we encounter Benoit Mandelbrot, fractals, parameterizations, a conical helix, butterfly curves, paradromic rings, Leonhard Euler, Antoine-Jean Lhuilier, chromatic numbers, projective planes, the four-color theorem, "The Island of Five Colors," Mobius's triangulated band, Johann Listing, homeomorphisms, ghosts, the fourth dimension, Immanuel Kant, Johann Carl Friedrich Zollner, Henry Slade, Alfred Schofield's "Another World," turning spheres and doughnuts inside out, optiverses, the Boy surface, cross-caps, Roman surfaces, the fantastic Mobius function, the Mertens conjecture, the Riemann zeta function, Mobius palindromes, the amazing o, coprimality, graph theory, hexaflexagons, Mobius shorts, Mobius tetrahedra, Mobius triangles, solenoids, Alexander's horned sphere, prismatic doughnuts, perfect square dissections, the squiggle map coloring puzzle, the cannibal torus, the pyramid puzzle, and Mobius in pop culture. Chapter 6 Cosmos, Reality, TranscendenceIn which we encounter nonorientable spaces, more enantiomorphs, dextrocardia with situs inversus, hyperspheres, Klein bottle coffee mugs, the world's largest Klein bottle, the Bonan-Jeener's Klein surface, Immanuel Kant redux, bilaterally symmetric Vernanimalcula guizhouena, the Babylonian god Marduk, Gottfried Wilhelm Leibniz, 3-tori, Max Tegmark, parallel universes, artificial life, simulated universes, John Horton Conway, the Wilkinson Microwave Anisotropy Probe, Gerhardus Mercator, the ekpyrotic model of universe formation and destruction, the Book of Genesis, self-reproducing universes, playing God, the pretzel transformation puzzle, and Mobius cosmoses. Chapter 7 Games, Mazes, Art, Music, and ArchitectureIn which we encounter Mobius chess, mazes, Knights' tours, Bishop domination on a Klein bottle chessboard, Mobius stairs and snow sculptures, Mobius buildings, Mobius postage stamps, Max Bill, LEGO sculptures beyond imagination, Mobius gear assemblies, complex knots, Teja Krasek, Mobius strips with Penrose tilings, Mobius music, Johann Sebastian Bach, Arnold Schoenberg, Nicolas Slonimsky, devil configurations, Mobius strips in psychology and human relations, and mazes played on Mobius strips. Chapter 8 Literature and MoviesIn which we encounter the literature of nonorientable surfaces, the "No-Sided Professor," "A. Botts and the Mobius Strip," "Paul Bunyon Versus the Conveyor Belt," "The Wall of Darkness," "A Subway Named Mobius," Gustavo Mosquera, The Secret Life of Amanda K. Woods, The Journey of Mobius and Sidh, The Lobotomy Club, Flatterland, Bana Witt's Mobius Stripper, Dhalgren, Marcel Proust's In Search of Lost Time, Six Characters in Search of An Author, "Time and the Conways," Donnie Darko, Femme Fatale, Mobius the Stripper, Vladimir Nabokov's The Gift, Coleman Dowell's Island People, Daniel Hayes's Tearjerker, Eugene Ionesco's The Bald Soprano, Solvej Balle's According to the Law, John Barth's Lost in the Funhouse, Paul Nahin's "Twisters," Martin Gardner's Visitors from Oz, ants trapped in Jordan curves, and Mobius in the suburbs. A Few Final WordsIn which we encounter Stanislaw Ulam, Franz Reuleaux, Georg Bernhard Riemann, Zen koans, Eternal Sunshine of a Spotless Mind, Harlan Brothers, Marjorie Rice, Roger Penrose, Arthur C. Clarke, the Mandelbrot set, an ambiguous ring, and Mobius strips in business and government. |
 Now at Amazon.Com
Now at Amazon.Com
|
Topology is about spatial relationships and glistening shapes that span dimensions. It's the Silly Putty of mathematics. Sometimes, topology is called "rubber-sheet geometry" because topologists study the properties of shapes that don't change when an object is stretched or distorted. The best way for people of all ages to fall in love with topology is through the contemplation of the Mobius strip -- a simple loop with a half twist….
Our nature is to dream, to search, and to wonder about our place in a seemingly lonely cosmos. Perhaps this is a reason that philosophers and writers have speculated about Mobius-shaped universes and higher dimensions, and what their inhabitants might be like. For many young, prospective scientists, the Mobius strip is a launch-pad to more sophisticated geometries and topological exploration…. The Mobius strip is the ultimate metaphor for something simple, yet profound -- something anyone could have discussed centuries prior to its discovery, but didn't. The Mobius strip is a metaphor for magic and mystery, and a perpetual icon that stimulates us to dream new dreams and look for depths even in seemingly shallow waters. |
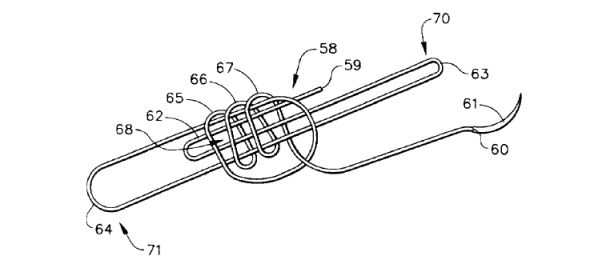
and knots like this one, which is patented for surgical use! |
50 First Dates, 182 Afghan bands, 3 Alexander's sphere, 100 Aliens and Mobius strips, 23-24 Ambiguous ring, 197-198, 208 Applications, 89 April Fool's joke, 71-72 Architecture, 155 Art, 154-170 Artificial life, 134 Asimov, Isaac, 37 Autism and knots, 15 Balle, Solvej, 186 Barth, John, 186 Barycentric calculus, 106-107, 111 Bill, Max, xx, 157 Borromean rings, 20-21 Boy surface, 82-83 Brown, Ronnie, 13 Browne, Cameron, 100-102 Business, 198 Butterfly curves, 64 Calculus, barycentric, 106-107, 111 Cantor set, 98 Celtic knots, 18 Chemistry, 51-58 Chess, 150-153 Chirality, 52-54 Christmas tree, 59, 167 Chromatic number, 69 Civilization and knots, 21 Clarke, Arthur, C., 174-175, 197 Collins, Stanley, 4 Coloring maps, 69-72, 108 Cosmos models, 111-119, 136-141, 193 Crosscap, 82-84 Crumey, Andrew, 188 Darwin, Charles, 36 Dehn, Max, 12 Devil's configuration, 170-171 Dhalgren, 179 Dietrich-Buchecker, Christiane, 54-55 DNA and knots, 17 Dodecahedral space, 131 Donnie Darko, 181 Dowell, Coleman, 184 Drugs, 52-56 Egan, Greg, 136 Einstein, Albert, 119 Ekpyrotic universe, 141 Elliot, Bruce, 188 Enatiomers, 54 Eozoon, 36 Escher, M. C., xx, 158 Eternal Sunshine, 194 Euclid, 117 Euler, Leonhard, 66-67, 74, 90, 103 Eversions, 79-81 Extrinsic geometry, 119 False dawn animal, 35-36 Fashion, Mobius, 60 Fauvel, John, xi, 26 Femme Fatale, 182 Fibonacci numbers, 85 Fiction, 40 Flat space, 138-139 Flood, Raymond, xi Four-color theorem, 70-72 Fourth dimension, 76, 116-117, 125-127 Fractals, 196, 213 Games, 146-153 Gardner, Martin, xxii, 3, 10, 71, 94, 174, 187, 196 Gauss, Carl, 28, 31, 73, 118 God, 142 Government, 198 Graph theory puzzle, 59 Graph theory, 93 Haken, Wolfang, 16 Handedness, 52-54 Hayes, Daniel, 184 Helix, 63 Hexaflexagons, 94 History and knots, 21 Hoidn, Phoebe, 17-18 Hole through hole, xv Homeomorphisms, 74-75, 199 Horned sphere, 100-102 Hyperbolic universe, 139 Hyperspace, 116-117, 125-127 Hypersphere, 119, 137 Infinite universe, 141 Inflation, 140 Intrinsic geometry, 119 Inventions, 39-60, 148 Ionesco, Eugene, 185 Jordan curves, 189 Josipovici, Gabriel , 183 Kalata, 56 Kells, Book of, 19 Kelvin, William, 16 Klein bottles, 69, 82, 105, 120-124, 129, 152-153, 160, 187-188 Kleinian group, 213 Knight's tours, 151, 155 Knots, 12-18, 77-78, 165 Borromean rings, 20-21 Celtic, 18 Chinese, 21 Chromatic number, 69 Civilization and, 21 Cutting, 14, 65 DNA, 17 Figure-eight, 16, 160 Fourth dimension, 77, 116 History and, 21 Homeomorphisms, 75, 100 Kells, Book of, 18 Mathematics, and 22 Molecules, 54-55 Patents, 50-51, 148 Perko, 14 Proteins, 18, 56 Puzzle, 22 Sailors, 21 Subatomic particles, 17-18 Trefoils, 12-18, 75, 162-163 Triquetra, 18 Unknot, 15 Vortex atom theory, 16-17 Krasek, Teja, 166-167 Longtin, Tom, 161-164 Language, 210 Lego, 158-160 Leibniz, Gottfried, 128 Leys, Jos, 14, 20, 213 Licentiousness, 38 Life, 134-135 Lipson, Andrew, 158-160 Lissajous curves, 63 Listing, Johann, 28, 73 Literature, 173-189 Luther, Martin, 26, 30 Ljubljana ribbon, 12 Magic, 2-4 Mandelbrot, Benoit, 196-197 Manifolds, 128, 137 Map coloring, 33, 69-72, 108 Matrix, 133-134 Maxwell, James, 17 Mazes, 37, 146-149, 209, 216 Mertens function, 87 Mirror worlds, 115-116 Mirror molecules, 52-54 Mirrored organs, 116 Mirrors, 125-127 Mobidromes, 91 Mobius Applications, 89 Bundles, 212, 215 Dualities, 212, 215 Fiber bundles, 212, 215 Function, 84-89 Groups, 212 Inversion formulas, 33, 212, 214 Nets, 33, 212 Statics, 33, 212 Tetrahedra, 96 Transform, 214 Transformations, 33, 212-213 Triangles, 97 Mobius, August, 25-35 Skull, xvii Place in history, 6, 197 Mobius, Paul, xvii, xviii, 27 Mobius, Karl August, 35-36 Mobius strip Aliens, 23-24 Architecture, 155 Art, xx, 154-170 Beer, xix Business, 198 Chemistry, 51-58 Chess, 150-153 Christmas tree, 59, 167 Coloring a side, 8 Cosmos, 143-144 Cutting, 9-10, 65 Fashion, 60 Fiction, 40 Government, 198 Language, 210 Lego, 158-160 Licentiousness, 38 Listing, Johann, 28 Literature, 173-189 Magical use, 2-4 Map coloring, 33, 69-72 Mazes, 37, 146-149, 209, 216 Molecules, 51-58 Movies, 173-189, 194 Music, 168-170 Parametric equations, 64 Patents, 39-60, 148 Penrose tiles, 166-167 Pop culture, 109 Proteins, 56 Psychology, 172 Religious use, 4 Sandwich, 11 Science metaphor, 36-37 Shorts, 95-96 Skiing, xix Snow sculpture, 168 Square dissections, 104-105 Stairs, 154-155 Stamps, 156-157 Suburbia, 190 Technology, 39-60 Toys, 147-149 Train tracks, 58 Triangulated, 72 Triple-thick, 10 Twist, number of, 11-12, 65 Mobius syndrome, 27-28 Molecular shapes, 51-58 See also Knots and Mobius strip Mosquera, Gustavo, 176 Movies, 173-189, 194 Multiple universes, 131-136, 141 Multiverse, 131-133 Music, 168-170 Nabokov, Vladimir, 184 Nahin, Paul, 187 Nelson, James, 3 Organs, mirrored 116 Orientability, 29, 82-83, 94, 114, 139 Palindromes, 90 Paradromic rings, 65 Parallel universes, 131-136, 141 Parametric equations, 62-65 Patents, 39-60, 148 Penrose triangle, 208 Penrose tiling, 166-167, 196 Perko knots, 14 Phillips, Dave, 37, 209, 216 Phrenology, xviii Pi, 86, 91-92 Pirandello, Luigi, 180-181 Polyhedron, 66-67 Pop culture, 109 Pretzel puzzle, 143 Priestly, John, 181 Primes, 86, 92 Prismatic doughnuts, 102-103 Projective plane, 69, 82, 105, 120, 129 Proteins, 18, 55 Proust, Marcel, 179-180 Psychology, 172 Puzzles Ambiguous ring, 197-198, 208 Ant planet, 189-190 Devil's configuration, 170-171 Graph, 59 Knot, 22 Maze, 37, 209, 216 Pretzel, 143 Pyramid, 109 Squiggle coloring, 108 Treadmill, 5 Pyramid puzzle, 109 Recycling symbol, xviii-xix Religion, 4 Reuleaux triangle, 42-43, 192 Riemann, Bernhard, 117, 193 Ring, ambiguous, 197-198, 208 Rivers, 92 Robinson, John, 13 Roman surface, 82-83 Rzepa, Henry, 57 Sailors and knots, 21 Sauvage, Jean-Pierre, 54-55 Scharein, Rob, 164-165 Schoenberg, Arnold, 169 Shoelaces, 51 Simanek, Donald, 208 Simulations, reality, 133-136 Simultaneous discovery, 29 Slapenarski surface, 174 Slonimsky, Nicolas, 169 Snow sculpture, 168 Solenoid, 97-99 Sphere eversions, 79-80 Sphere, horned, 100-102 Square number, 84 Squareful numbers, 85 Squiggle map coloring, 108 Stairs, 154-155 Stamps, 156-157 Star Trek, 177 Stasiak, Andrzej, 17-18 Stephens, Nicky, 154-155 Steward, Ian, 1, 6, 145, 191 String theory, 90 Suburbia, 190 Subway, 176 Surgical knots, 51 Symmetry, 125-126 Technology, 39-60 Tegmark, Max, 132 Thalidomide, 54 Three-torus, 128-130, 140 Time travel, 182-183 Tissandier, Gaston, 3 Topology, xvi, 61-84 Torus eversions, 79-81 Torus, 69, 79-82, 105, 128-130, 154 Toys, 147-149 Treadmill puzzle, 5 Train tracks, 58 Trefoil knot, 12-17, 75, 162-163 Triangle, Reuleaux, 42-43, 192 Triangles, 117-118 Triquetra, 18 Twists in Mobius strips, 11-12, 65 Universe models, 111-119, 136-141, 193 Unknot, 15 Upson, William, 175 Vortex atoms and knots, 16-17 Walba, David, 52-53 Wilson, Robin, xi Witt, Bana, 179 Zelazny, Roger, 40 Zollner, Johann, 77-79 |

High-tech assortment of Mobius Christmas tree ornaments Courtesy of Teja Krasek .
.
|