Contact |
News! |
Books |
Home |
Contact |
News! |
Books |
Home |

Order from Amazon.com. |
to the time of Newton, what he has done is much the better half." -- Gottfried Wilhelm Leibniz, co-discoverer of calculus "If I have seen further than others, it is by standing upon the shoulders of giants." -- Isaac Newton, the other discoverer of calculus "If I have not seen as far as others, it is because giants were standing on my shoulders." -- Hal Abelson, MIT Professor |
 Click here
to see the book at Amazon.Com!
Click here
to see the book at Amazon.Com!
 Impress Friends!
Impress Friends!
 Expand Your Mind!
Expand Your Mind!
 The mysterious, quirky, and fun puzzles in this book should cause even the most left-brained readers to fall in love with calculus. The antics of Luigi, Fiona, Rosario, and Big Tony will entertain people at all levels of mathematical sophistication. In fact, this book focuses on creativity, discovery, and challenge.
The mysterious, quirky, and fun puzzles in this book should cause even the most left-brained readers to fall in love with calculus. The antics of Luigi, Fiona, Rosario, and Big Tony will entertain people at all levels of mathematical sophistication. In fact, this book focuses on creativity, discovery, and challenge.
 One of the abiding sins of mathematicians is an obsession with completeness -- an urge to go back to first principles to explain their works. As a result, readers must often wade through pages of background before getting to the essential ingredients. To avoid this burden, each chapter in this book is short. You'll quickly get the essence of a technique or question. A number of the basic methods and challenges are representative of a wider class of problems of interest to mathematicians today. One advantage of this brief format is that you can jump right in to experiment and have fun, without having to sort through a lot of detritus. Thus, this book is not intended for mathematicians looking for formal mathematical explanations. Of course, this approach has some disadvantages. In just a few pages, Luigi can't go into any depth on a subject. You won't find much historical context, philosophy, or extended discussions. You won't find proofs and derivations; I simply present most of the important formulas. The focus is on procedures and drills for solving problems and not on some of the deeper meanings of calculus.
One of the abiding sins of mathematicians is an obsession with completeness -- an urge to go back to first principles to explain their works. As a result, readers must often wade through pages of background before getting to the essential ingredients. To avoid this burden, each chapter in this book is short. You'll quickly get the essence of a technique or question. A number of the basic methods and challenges are representative of a wider class of problems of interest to mathematicians today. One advantage of this brief format is that you can jump right in to experiment and have fun, without having to sort through a lot of detritus. Thus, this book is not intended for mathematicians looking for formal mathematical explanations. Of course, this approach has some disadvantages. In just a few pages, Luigi can't go into any depth on a subject. You won't find much historical context, philosophy, or extended discussions. You won't find proofs and derivations; I simply present most of the important formulas. The focus is on procedures and drills for solving problems and not on some of the deeper meanings of calculus.
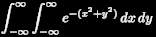 . These strange symbols impressed the heck out of me. I wondered if I would I ever be able to understand what an integral was. My father's books provided a seed from which my interest in calculus grew, and, along with my love of pizza, provided an early stimulus for Calculus and Pizza.
. These strange symbols impressed the heck out of me. I wondered if I would I ever be able to understand what an integral was. My father's books provided a seed from which my interest in calculus grew, and, along with my love of pizza, provided an early stimulus for Calculus and Pizza.
 Calculus and Pizza is for anyone who has pondered what calculus is all about, for students who want to do well on exams and get into good colleges or graduate schools, and for lay people who want to get just a taste or a refresher course. The book might most effectively be used as a supplement to a traditional calculus text. If you've not taken calculus for a few years, then Calculus and Pizza can serve as a quick review of some of the essential rules, formulas, and problems. I assume that the reader is familiar with high school algebra and some of the basic rules of trigonometry.
Calculus and Pizza is for anyone who has pondered what calculus is all about, for students who want to do well on exams and get into good colleges or graduate schools, and for lay people who want to get just a taste or a refresher course. The book might most effectively be used as a supplement to a traditional calculus text. If you've not taken calculus for a few years, then Calculus and Pizza can serve as a quick review of some of the essential rules, formulas, and problems. I assume that the reader is familiar with high school algebra and some of the basic rules of trigonometry.
| "Today, calculus has invaded every field of scientific endeavor and plays invaluable roles in biology, physics, chemistry, economics, sociology, engineering -- and in any field where some quantity, like speed or temperature, changes. Calculus can be used to help explain the structure of a rainbow, teach us how to make more money in the stock market, guide a spacecraft, make weather forecasts, predict population growth, design buildings, quantify happiness, and analyze the spread of AIDS. Calculus has caused a revolution. It has changed the way we look at the world." -- Cliff Pickover |
 Table of Contents
Table of ContentsPreface Introduction 1. Pizza Velocity and the Derivative 2. Derivative Definitions and Rules 3. Derivatives and Slopes 4. Rules for Products and Quotients 5. Chain Rule and Implicit Differentiation 6. Maxima and Minima 7. Min Max Pizza Applications 8. Exponentials and Logarithms 9. Limits and Continuity 10. Related Rates 11. Integration 12. Logarithmic Differentiation, Integration by Parts, Trigonometric Substitution, and Partial Fractions 13. Exponential Growth and Decay 14. Calculus and Computers 15. Multiple Integrals 16. Calculus in a Nutshell 17. Luigi's Mind-Boggling Workout Routine Conclusion Answers to Odd-Numbered Exercises Further Reading

 Index
IndexAbelson, Hal, vii answers to problems, 157-204 antiderivatives, 93-94, 101, 104 applications (of calculus) 6-7, 12, 138-139 area, and integrals, 97 area between two curves, 99 Barrow, Isaac, xiii base changes, 58 Berkeley, George, xii Bolyai, Janos, xiv Burton, David, xi calculus applications of, 6-7, 12, 138-139 first use of symbols, xiv, 13 first textbook on, xiv fundamental anagram of, 155 fundamental theorem of, 97 history of, xii-xiv chain rule, 25-34 exponential, 62 logarithmic, 62 trigonometric, 29-30 Child, Julia, xi, 1 computers calculus and, 127-134 programs, 69-70, 129, 132 concavity, 41-43 concave up and down, 42 conclusion, 155-156 continuity, 65-79 definition, 73, 75 cosine rules, 29-30 critical points, 37-39, 47 Darwin, Charles, xiv decay, exponential, 119-126 decreasing functions, 36 definite integrals, 95, 105 derivatives, xiii, 3-7, see also chain rule definitions, 9-14, 128 first use of symbol, xiv, 13 rules, 9-14, 21-34, 58 slopes, 17-20, 36 velocity, 3-7 Descartes, Rene, xiii differential equations, 121 differentiablity, of functions, 77 differentiation, see also derivatives logarithmic, 107-109 e (Euler's number), 59-61 exercises, additional, 151-153 exponential rule, 62 exponential growth and decay, 119-126 exponentials, 57-64 extended power rule, 27 fluxions, xii, 156 formulas, summary of, 141-149 fractal, 74-74 functions, increasing and decreasing, 36 fundamental theorem of calculus, 97 God's formula, 61 growth, exponential, 119-126 history of calculus, xii-xiv implicit differentiation, 30-34, 82 increasing functions, 36 indefinite integrals, 95, 101, 104 indeterminate form, 71 infinitesimals, xiv, 13 inflection points, 37-40 integrals area, 97 definite, 95, 101, 104 definition of, 95 first use of symbol, xiv indefinite, 95, 101, 104 multiple, 135-139 integration, xii, xiv, 93-106 by parts, 110-111 partial fractions, 114-116 Riemann, 97 rules, 99, 101 trigonometric substitution, 111-112 intervals, 47-48, 53 Kammerer, Paul, xiv Koch curve, 74-75, 76 Leibniz, Gottfried, vii, xiii-xiv, 13, 155-156 L'H˘pital's rule, 71-74 limits, 10, 18, 65-79, 128 local minima and maxima, 37-39, 47-48 logarithm rules, 58, 62 logarithmic differentiation, 107-109 logarithms, 57-64 maxima and minima, 35-44, 47-48 local, 37-39, 47-48 menu, calculus, 66 min-max applications, 45-55 multiple integrals, 135-139 multiplier rule, 10 Newton, Isaac, vii, xiii-xiv, 13, 155-156 partial fractions, 114-116 parts (integration by), 110-111 power rule, 10, 27 extended, 27 product rule, 21-24 quotient rule, 21-24 ranges, 48 related rates, 81-91 Riemann integrals, 97 rule summary, 141-149 second derivative test, 38-39 sine rules, 29-30 slopes (and derivatives), 17-20, 36 sum rule, 10 summary of formulas, 141-149 tangent lines, 18, 36 trigonometric chain rules, 29-30 trigonometric derivatives, 29-30 trigonometric substitution, 111-112 velocity, 3-7 Wallis, John,xiii workout routine, 151-155