with the constraints
f(0.5)
= 1
f '(0.5) = 0
f(1) = 0
f '(0) = 4
where f ' = df/dx. Note that the form of the function also guarantees that f(0) = 0. The constraints ensure that the function maps the unit interval (0,1) back onto itself twice, with a consequent chaotic dynamic covering the entirety of the unit interval upon repeated iteration.
The constraints lead to the following transcendental equations:
f '(0.5) = 0
f(1) = 0
f '(0) = 4
where f ' = df/dx. Note that the form of the function also guarantees that f(0) = 0. The constraints ensure that the function maps the unit interval (0,1) back onto itself twice, with a consequent chaotic dynamic covering the entirety of the unit interval upon repeated iteration.
The constraints lead to the following transcendental equations:
b1
tanh(a1/2) + b2 tanh(a2/2) = 1
a1b1 sech2(a1/2) + a2b2 sech2(a2/2) = 0
b1 tanh(a1) + b2 tanh(a2) = 0
a1b1 + a2b2 = 4
It turns out that all four equalities cannot be simultaneously satisfied. However, they are most nearly satisfied if a2 is very small and b2 is very large so that a2b2 = c is finite, in which case the first three equations reduce to
a1b1 sech2(a1/2) + a2b2 sech2(a2/2) = 0
b1 tanh(a1) + b2 tanh(a2) = 0
a1b1 + a2b2 = 4
It turns out that all four equalities cannot be simultaneously satisfied. However, they are most nearly satisfied if a2 is very small and b2 is very large so that a2b2 = c is finite, in which case the first three equations reduce to
b
tanh(a/2) + c/2 = 1
ab sech2(a/2) + c = 0
b tanh(a) + c = 0
where the subscripts have been dropped on a1 and b1. Then, by
nonlinear regression, using a variant of simulated annealing, the
parameters are determined to be:ab sech2(a/2) + c = 0
b tanh(a) + c = 0
a
= 1.42668906710772...
b = 5.97811605717192...
c = -5.32641819604181...
The resulting iterated map is thus
Note that the linear growth rate f '(0) = ab + c = 3.20249462462648... in contrast to the logistic map for which f '(0) = 4.
The computer program that was used to calculate these values is available in PowerBASIC source and executable code, and the resulting map (in cyan) is compared with the logistic map (in black) below:
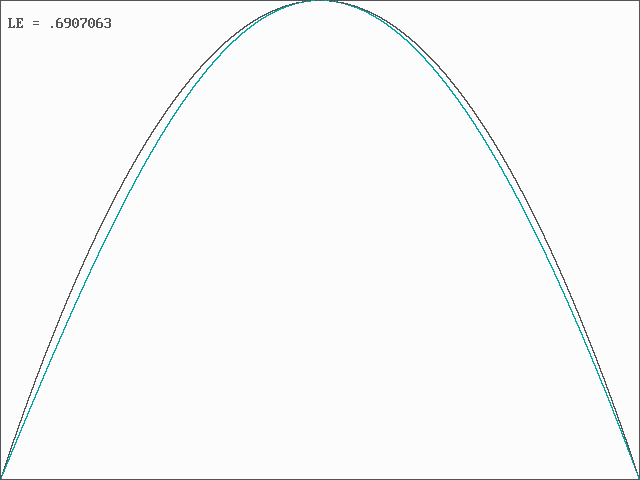
The system has a Lyapunov exponent (base e) of 0.6907063..., which is slightly smaller than the logistic map for which the Lyapunov exponent is ln(2) = 0.693147181... but larger than the sine map for which the Lyapunov exponent is 0.689067... (see J. C. Sprott, Chaos and Time-Series Analysis, Oxford, 2003).
A least squares fit of the four coefficients to 1000 iterates of the logistic map gives the slightly different mapping:
b = 5.97811605717192...
c = -5.32641819604181...
The resulting iterated map is thus
xn+1
= 5.97811605717192 tanh(1.42668906710772xn) - 5.32641819604181xn
Note that the linear growth rate f '(0) = ab + c = 3.20249462462648... in contrast to the logistic map for which f '(0) = 4.
The computer program that was used to calculate these values is available in PowerBASIC source and executable code, and the resulting map (in cyan) is compared with the logistic map (in black) below:

The system has a Lyapunov exponent (base e) of 0.6907063..., which is slightly smaller than the logistic map for which the Lyapunov exponent is ln(2) = 0.693147181... but larger than the sine map for which the Lyapunov exponent is 0.689067... (see J. C. Sprott, Chaos and Time-Series Analysis, Oxford, 2003).
A least squares fit of the four coefficients to 1000 iterates of the logistic map gives the slightly different mapping:
xn+1
= 5.821 tanh(1.487xn)
- 23.942 tanh(0.2223xn)
with a mean square error of 3.249 × 10-4, although it is still slowly converging as the second term approaches ever more closely a linear function.
with a mean square error of 3.249 × 10-4, although it is still slowly converging as the second term approaches ever more closely a linear function.