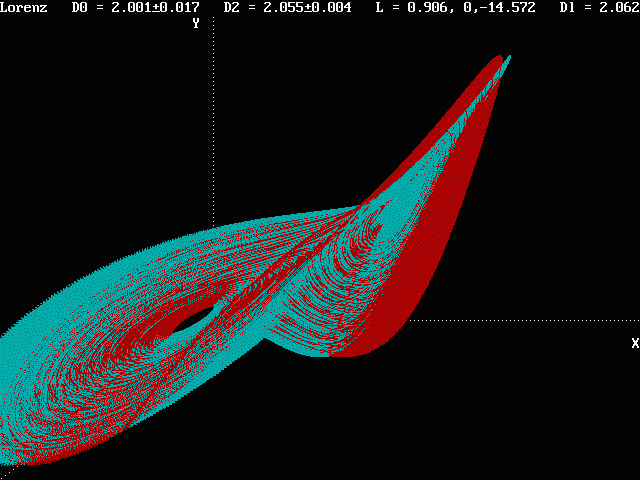
The Lorenz attractor is given by the following 3-dimensional system of ordinary differential equations:

In his orginal paper [E. N. Lorenz, J. Atmos. Sci. 20, 130 (1963)], Lorenz used the parameters p = 10, r = 28, and b = 8/3 for which the trajectories produce a strange attractor.

    For reasons unknown, published calculations of the largest Lyapunov exponent for the Lorenz attractor [see for example, A. Wolf, J. B. Swift, H. L. Swinney, and J. A. Vasano, Physica 16D, 285 (1985)] have usually used the values p = 16, r = 45.92, and b = 4 for which the Lyapunov exponents (base-2) are (2.16, 0, -32.4).  It is more natural to express the exponents for a flow in base-e, in which case the values are (1.50, 0, -22.46).  For a flow, one of the exponents must be zero and the sum of the exponents is -p - 1 - b = -21, which is approximately satisfied by the quoted results.

    Reported here is a numerical calculation of the largest Lyapunov exponent for the Lorenz attractor using Lorenz's original parameters.  The calculation was performed in a several-day run on a 200-MHz Pentium Pro using a PowerBASIC program available in both source and (DOS) executable code.  The program uses the fourth-order Runge-Kutta method with a fixed step size of 0.001, and performed over 10⁹ iterations, corresponding to a maximum time of over 10⁶.  More details on the numerical calculation of the Lyapunov exponent are available.  Output from the program is shown below:

    The image above shows the Lorenz attractor as an anaglyph that can be viewed in 3-D using red-blue glasses.  The values of the Lyapunov exponents are (0.906, 0, -14.572).  From these exponents, the Kaplan-Yorke dimension can be calculated from D_KY = 2 + l₁ / |l₃| = 2.062.  The program also calculates the capacity dimension D₀ = 2.001 ± 0.017 and the correlation dimension D₂ = 2.055 ± 0.004, but these values are considerably less reliable than the Kaplan-Yorke dimension, which is believed to be accurate to the four significant digits quoted.  In particular, it is known that D₀ cannot be less than D₂.  In addition to the statistical errors quoted above, there are systematic errors particularly in the calculation of D₀ arising from the rather crude box size of 100 x 100 x 100 used in the capacity dimension calculation.

For a more recent and more accurate calculation see the Lyapunov Exponent Spectrum Software.